Springen Sie zu einem Abschnitt unten:
Das Wichtigste bei der Prüfung von Bauteilen mit einem Frequenzgang über 100 MHz sind ein guter Netzwerkanalysator und sorgfältig konstruierte Prüfvorrichtungen für die Kalibrierung sowie für die eigentliche Prüfung. Das Gleiche gilt für die Prüfung im Zeitbereich. Bei der Messung der Anstiegszeitcharakteristik muss man sich der Über- und Unterschwinger des Anstiegszeitimpulses bewusst sein, die die Signalqualität nachteilig beeinflussen können.
Das Design der Halterung beginnt mit geeigneten SMA-Steckverbindern auf Hochfrequenz-Plattenmaterial. Es gibt verschiedene Materialien, die dafür geeignet sind, darunter FR-4, G-Tech-Materialien und
verschiedene PCB-Materialien von Rogers. Viele sind der Meinung, dass FR-4-Material geeignet ist, da der Nullstellungsprozess der Halterung die Hochfrequenzverluste eliminiert. Als allgemeine Regel gilt: Unter 6 GHz ist es in Ordnung; über 6 GHz verbessert die Verwendung von Rogers Hochfrequenz-Schaltungsmaterialien wie RO3203 oder RO4350 die Testleistung. Je nach TCE-Anpassung der Komponente(n) oder Leistungsanforderungen bietet Rogers verschiedene andere Materialien an. Die meisten dieser Materialien sind keramikgefüllt.
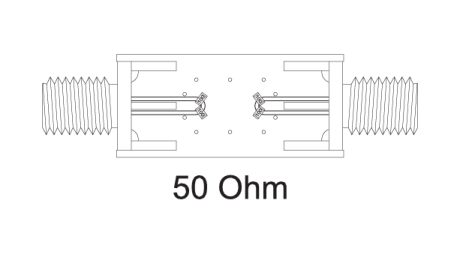
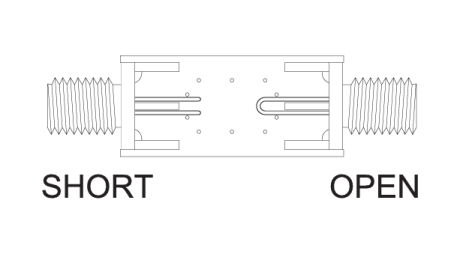
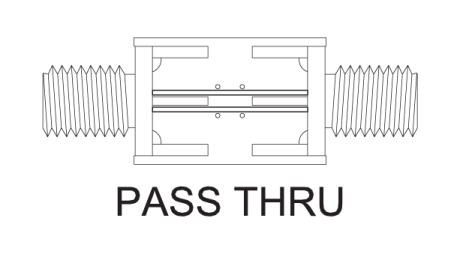
Die Abbildungen 6, 7, 8 und 9 zeigen das Layout der Kalibrierungsplatine für einen Kurzschluss gegen Masse, einen offenen Stromkreis, eine Durchgangsleitung, einen 50-Ohm-Impedanzabschluss und das für die Prüfung des Geräts verwendete Layout. Es wurden so viele Massepunkte wie möglich verwendet und scharfe Ecken vermieden. Alle Signalpfadübergänge wurden so allmählich wie möglich gestaltet.
Nach Abschluss der Kalibrierungstests wurde der Test mit einem Agilent Network Analyzer, Modell 8720ES, wie folgt durchgeführt (siehe Testlayout in Abbildung #4).
Alle Kalibrierungsplatinen wurden in den Netzwerkanalysator eingegeben und gespeichert. Das zu prüfende Relais wurde dann gemessen und gespeichert. Die Kalibrierungsdaten wurden dann eingegeben und
Die Kalibrierungsdaten wurden dann eingegeben und die Verluste aufgrund der Platine in den verschiedenen Konfigurationen wurden extrahiert. Diese wurden mit Daten verglichen, die aus einem MIMICAD-Programm unter Verwendung der dargestellten Ersatzschaltung und der S-Parameter extrahiert wurden; es zeigte sich, dass beide sehr genau übereinstimmten.
Sehen Sie sich die Ergebnisse der unten gezeigten Daten aus dem Netzwerkanalysator an. Eingeschlossen sind die Isolation, die Einfügungsdämpfung und das VSWR. Außerdem finden Sie unten ein Smith-Diagramm, das die Impedanz für eine bestimmte Frequenz über den gesamten Frequenzbereich anzeigt.
Entwurf der Halterung
Der erste wichtige Schritt ist die Festlegung der genauen Geometrie der Prüfvorrichtung. Im Folgenden sind vier Geometrien und die entsprechenden Gleichungen zur Berechnung der
charakteristischen Impedanz.
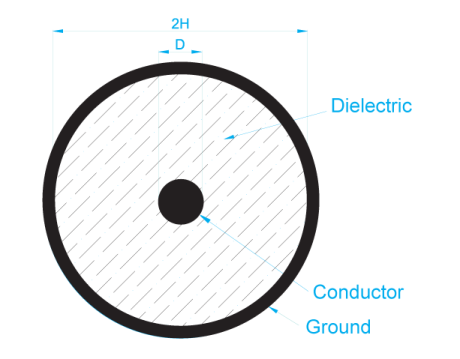
Zo = 60/(√ (εr)) ln ((2h)/d)
Gleichung #5 (für ein Koaxialkabel)
Dabei sind h und d wie oben definiert und εr ist die Dielektrizitätskonstante für das Material zwischen den Leitern.
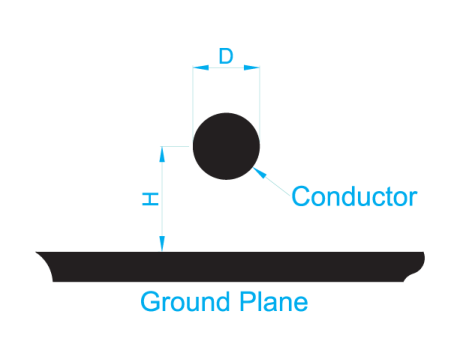
Zo = 60/(√ (εr)) ln ((4hkp)/d)
Gleichung #6 (für einen runden Draht über einem Boden) für einen runden Draht über einem Boden
Hier ist kp der Näherungsfaktor für einen runden Draht über der Erde, der nahe bei Eins liegt, wenn das Verhältnis h/d groß ist; bei engen Abständen beträgt er jedoch ungefähr
kp = ½ + (√ (4h2 – d2))/4h
Gleichung #7
kp wird auf ½ reduziert, wenn der runde Draht den Boden bei d = 2h berührt. Der Proximity-Effekt beruht auf demselben Mechanismus wie der Skin-Effekt. Die gegenseitige Abstoßung treibt gleichartige Ströme zu den äußersten Rändern der einzelnen Leiter, die den Strom in die entgegengesetzte Richtung führen. Dadurch wird der Strom in runden Drähten zu der Seite gedrängt, die der Erde am nächsten liegt. Wie beim Durchgang des Signals durch das Relais sind der Nahbesprechungseffekt und der Skineffekt bei einer Koaxialleitung nicht zu unterscheiden, da sich die gesamte Oberfläche des runden Mittelleiters im gleichen Abstand von der Abschirmung befindet. Bei dünnen rechteckigen Leitern wird der Annäherungseffekt normalerweise nicht berücksichtigt, aber der Skineffekt treibt die Ströme zu den Kanten der Leiter.
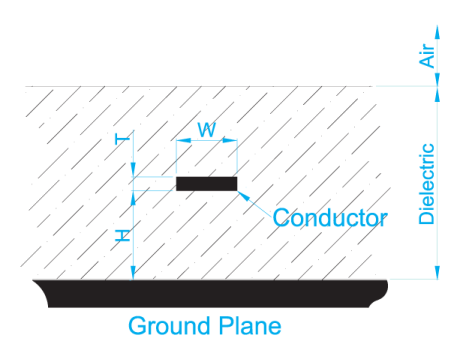
Zo = 60/(√ (εr)) ln ((5,98h)/(0,8w + t))
Gleichung #8 (vergrabene Mikrostreifenleitung über Erde)
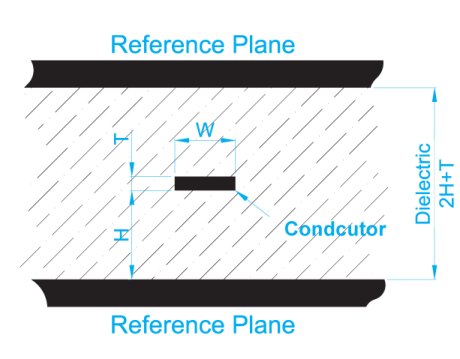
Zo = 60/(√ (εr)) ln (3,8(h +0,5t)/(0,8w + t))
Gleichung #9 (Streifenleitung zwischen Masseebenen)
Testaufbau und Testvorrichtungen
Der Schlüssel zum korrekten Testen einer Komponente in einem HF-Schaltkreis ist die richtige Verwendung von Prüfvorrichtungen.
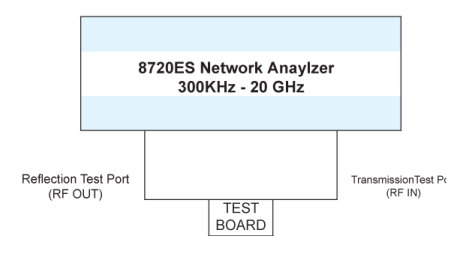
Kalibrierungsansatz kritisch
Die Vorrichtungen wurden so konstruiert, dass sie als Kalibrierungsplatinen dienen, um eine bessere Charakterisierung der Relais zu ermöglichen. Alle für die Prüfung der zu prüfenden Relais (RUT) verwendeten Vorrichtungsplatinen verwenden SMA-Steckverbinder für die Verbindung zu und von den Prüfgeräten sowie für die Anschlüsse. Im Folgenden wird der Aufbau der zu prüfenden Platinen beschrieben:
- RUT kalibriert mit einer 50 Ohm Leitung und offenem Abschluss
- RUT kalibriert mit einer 50-Ohm-Leitung und kurzgeschlossenem Anschluss
- RUT kalibriert mit einer 50-Ohm-Leitung und einem 50-Ohm-Abschluss
- RUT kalibriert mit einer 50-Ohm-Durchgangsleitung
Testergebnisse
Die Abbildungen 10 bis 16 zeigen die Ergebnisse unserer Tests mit den zuvor beschriebenen Verfahren und den vorgestellten Vorrichtungen. Die verwendeten Halterungen wurden aus
FR-4-Leiterplattenmaterial. Eine Verbesserung der Halterung unter Verwendung von Rogers PCB-Material könnte die Ergebnisse verbessern.
Einfügedämpfung
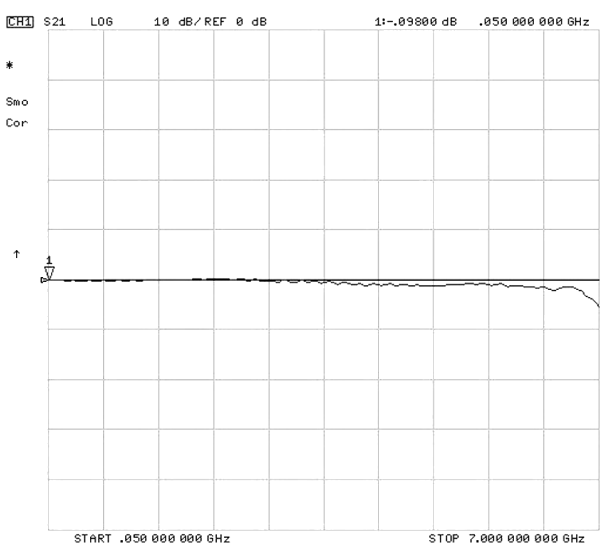
Wie bereits erläutert, ist die Einfügungsdämpfung der Verlust an Leistung, der durch das Relais geht. Die Einfügedämpfung ist eine der wichtigsten Messungen im HF-Bereich, da sie einfach ein Maß für den Verlust des Signals ist, das durch die Komponente (Reed-Relais) geht. Die Minimierung dieses Verlustes ist ein zentrales Anliegen.
Zunächst ist deutlich zu erkennen, dass die Einfügedämpfung bis 7 GHz hervorragend ist, wie in Abbildung 10 zu sehen ist . Wie gezeigt, ist die Einfügungsdämpfungskurve sehr flach und beginnt bei 7 GHz abzufallen. Dies deutet eindeutig darauf hin, dass Signale, ob digital oder analog, beim Schalten und Durchlaufen dieses CRF-Keramik-Reed-Relais sehr gut abschneiden werden. Bei der Verwendung von Halbleitern als Schaltelement kann es manchmal zu Intermodulationsverzerrungen kommen, die zu Verzerrungen im Frequenzgang führen. Bei einem passiven Bauelement wie dem Reed-Relais gibt es keine Intermodulationsverzerrungen, was zu einer sehr flachen Einfügungsdämpfung bis zu 7 GHz führt. Diese sehr flache Einfügungsdämpfung ermöglicht es dem Benutzer, eine Vielzahl verschiedener Frequenzen oder digitaler Impulse unterschiedlicher Breite zu schalten, zu übertragen oder zu verarbeiten.
ohne sich Gedanken über verschiedene Schalter für die unterschiedlichen Frequenzen machen zu müssen.
Einfügungsdämpfung von Kupferdrähten

Es wurde vorgeschlagen, dass ein Reed-Relais bei höheren und höheren Frequenzen keine sehr guten Leistungseigenschaften aufweist, da es Nickel/Eisen als Mittelleiter verwendet. Oft wird der Skin-Effekt als Schuldiger vorgeschlagen, da Nickel und Eisen als ferromagnetische Stoffe eine hohe magnetische Permeabilität μ haben. Dies ist jedoch nicht der Fall, wie in Abbildung 11 gezeigt wird, wo der Reed-Schalter in Abbildung 9 durch einen reinen Kupferdraht ersetzt wurde.
Vergleicht man die Abbildungen 10 und #11, so sieht man nur einen geringen oder gar keinen Unterschied. Unter hohen Leistungsübertragungsbedingungen würde man wahrscheinlich einen Unterschied feststellen. Aber wie bei vielen Anwendungen ist die zu schaltende Leistung sehr gering, so dass wir nur bis 7 GHz einen vernachlässigbaren Effekt sehen.
VSWR
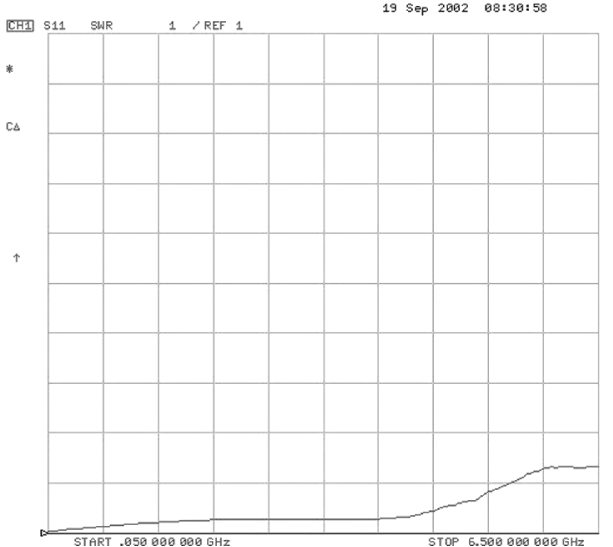
.
VSWR stellt die Auswirkungen der Leistungsübertragung durch stehende Wellen dar. Wenn stehende Wellen auf einer Leitung vorhanden sind, wird ein Teil der Leistung auf die Leitung zurückreflektiert und von der Quelle erneut reflektiert. Diese hin- und hergehende Reflexion erzeugt stehende Wellen. Diese stehenden Wellen stören die Übertragung der ursprünglichen Signale von der Quelle, da sie ständig vorhanden sind und kontinuierlich Leistung absorbieren. Abbildung 12 zeigt das VSWR für das Reed-Relais. Obwohl es immer noch ein wichtiges HF-Merkmal
für die Analyse analoger kontinuierlicher Wellen ist, wird die Einfügedämpfung eher für HF-Eigenschaften betrachtet.
Isolierung
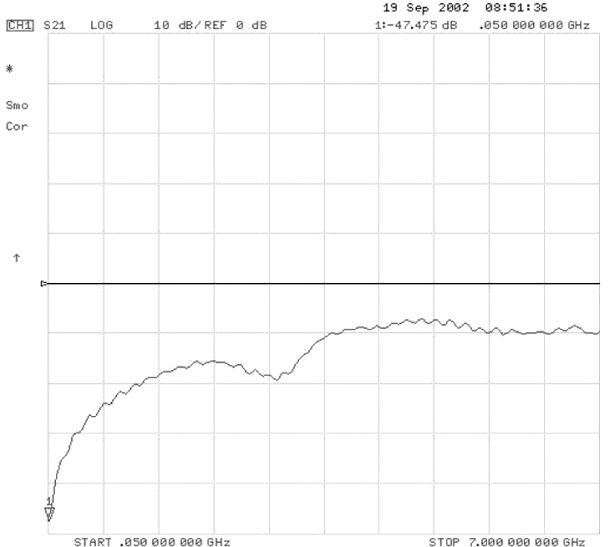
Vertikale Skala: 10 dB/div bezogen auf die 0-Marke.
Isolation ist die Fähigkeit einer Komponente, das HF-Signal von der weiteren Ausbreitung in einem Schaltkreis zu isolieren. Für ein Reed-Relais ist die Isolation ein Maß für die Fähigkeit, die weitere
Ausbreitung des Signals zu verhindern, wenn es sich im offenen Zustand befindet. Wir alle denken, dass ein Schalter im offenen Zustand bedeutet, dass kein Signal über diese offenen Kontakte hinausgeht. Bei HF wissen wir jedoch, dass ein offener Stromkreis nicht völlig offen ist, weil die Kapazität über den Kontakten einen Leckpfad darstellt; und bei ausreichend hohen Frequenzen tritt genau das ein. In Abbildung 13 ist eine Isolierung von -50 dB oder mehr bei niedrigen HF-Frequenzen zu sehen, die bei 3 GHz auf -15 dB abfällt und bei 7 GHz auf -10 dB sinkt. Zu diesem Abfall der Isolation trägt der Kontaktabstand bei. Eine Vergrößerung des Kontaktabstands beim Reed-Schalter ist sehr schwierig, da dies eine größere Kapsel erfordern würde, was wiederum die Gehäusegröße erhöhen würde. Außerdem macht ein größerer Spalt den Schalter weniger empfindlich beim Schließen, so dass mehr Spulenleistung erforderlich ist. Wenn die Isolierung ein kritischer Parameter in einer Anwendung ist, hilft es, mehr als ein Reed-Relais aneinanderzureihen. Auch die Verwendung eines ‚T‘-Schalters
oder eines halben T-Schalters lassen sich wesentlich höhere Isolationswerte erzielen.
Rückflussdämpfung

Vertikale Skala: 10 dB/div, bezogen auf die 0-Marke.
Die Rückflussdämpfung ist ebenfalls ein HF-Parameter, der nicht so häufig verwendet wird wie die Einfügedämpfung oder die Isolierung. Wie bereits erwähnt, ist sie ein Maß für die Leistung des HF-Signals, das zur Quelle zurückreflektiert wird.
zurück zur Quelle reflektiert wird. Wie in Abbildung 14 zu sehen ist, beträgt die Rückflussdämpfung nur 35 db des reflektierten Signals bei den niedrigen Frequenzen und etwa 10 db, die bei 6,5 GHz zurückgeworfen werden.
Dabei gilt: Je höher der dB-Wert, desto geringer der Anteil des reflektierten Signals.
Charakteristische Impedanz
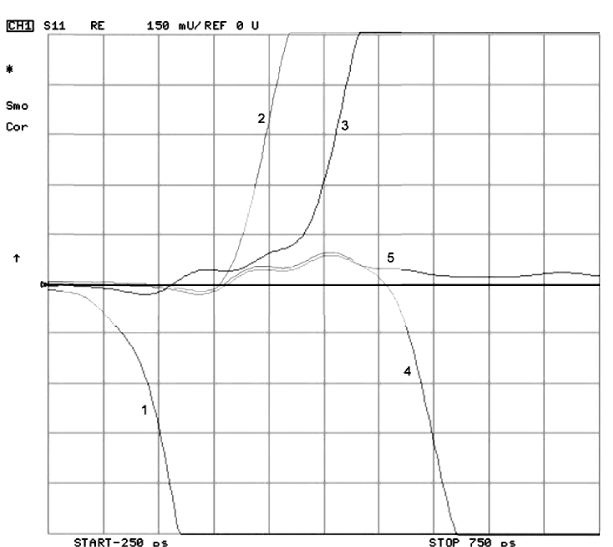
Um die meisten Informationen aus einer Messung der charakteristischen Impedanz des Relais zu gewinnen, ist es sinnvoll, Messungen des Signals bis zu bestimmten Punkten durchzuführen, während es durch das Relais läuft. Da diese Messung eine räumliche Messung ist, kann die tatsächliche Impedanz an jedem Punkt des Relais gemessen werden. Die folgenden Bezugspunkte wurden wie in Abbildung 15 dargestellt gewählt:
- Ein Kurzschluss vor dem Relais, der definiert, wann das Signal in das Relais eintritt
- Offene Kontakte definieren das Signal bis zur Mitte des Relais
- Geschlossene Kontakte definieren den Signalweg bis zum Ende des Relais
- Geschlossene Kontakte mit einem Kurzschluss am Relais
- Geschlossene Kontakte mit dem Relais schließen mit 50 Ohm ab
Überlagert man die 5 Leiterbahnen mit der tatsächlichen Leiterbahn durch das Relais, erhält man ein vollständiges Bild des Wellenwiderstands an jedem Punkt des Relais. Dies ist sehr
wertvoll, insbesondere wenn das Relais oder die Komponente leicht von der 50-Ohm-Impedanz abweicht. Wie aus der Kurve in Abbildung 15 hervorgeht, liegt das Relais leicht über 50 Ohm. Da die Kurve hoch ist, deutet dies auf einen leicht induktiven Eingang in und aus dem Relais hin. Durch Kompensation mit einer kleinen Kapazität an jedem Ende des Relais kann die
Impedanz auf den gewünschten Wert. Dies wiederum verbessert die Leistung des Relais in einer bestimmten Schaltung und erhöht auch seine Leistung bei höheren HF-Frequenzen.
Smith-Tabelle
- 1 – Kurzschluss vor dem Relais
- 2 – Offene Kontakte
- 3 – Geschlossene Kontakte
- 4 – Geschlossene Kontakte – kurzgeschlossen
- 5 – Geschlossene Kontakte – 50 Ohm
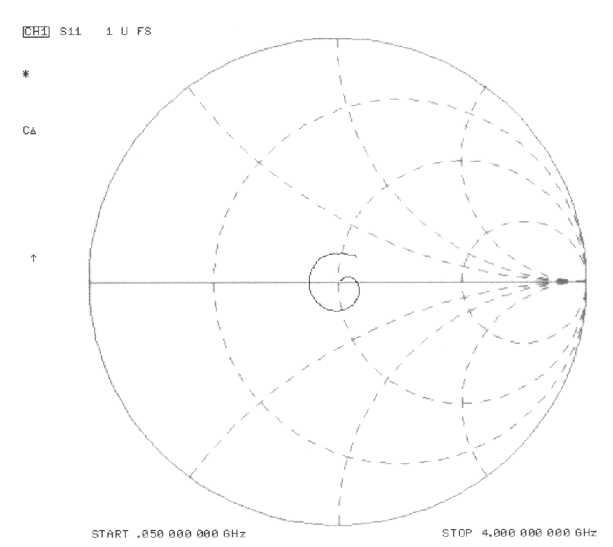
Wenn man verschiedene HF-Frequenzen in einer bestimmten Anwendung oder bei einer bestimmten Frequenz betrachtet, kann ein Smith-Diagramm helfen, indem es die charakteristische Impedanz über einen
gegebenen Frequenzbereich. Das Smith-Diagramm zeigt den Frequenzgang für Frequenzen von 50 KHz bis zu 4 GHz an. In Abbildung 16 ist die Darstellung der Punkte um den realen 50-Ohm-Punkt zentriert. Zum besseren Verständnis dieses Smith-Diagramms ist der zweite gepunktete Kreis, der vom rechten Mittelpunkt des großen Kreises ausgeht, der 50-Ohm-Impedanzkreis. Die Mittellinie des Kreises, die horizontal verläuft, ist die reelle Achse. Darstellungen oberhalb dieser Linie sind induktiv und Darstellungen unterhalb dieser Linie sind kapazitiv. Wie gezeigt, befindet sich die Darstellung des CRF-Relais in einem engen Kreis um die reelle Achse und ist um die 50-Ohm-Kreisachse zentriert.
.
Zusammenfassung
Wie man sieht, ist das CRF-Reed-Relais ein ausgezeichnetes Reed-Relais zum Schalten und Übertragen von HF-Signalen mindestens bis zu 7 GHz und darüber hinaus. Derzeit bemühen wir uns, seine Eigenschaften bis zu 10 GHz und darüber hinaus zu verbessern. Dies ist ein erreichbares Ziel, da wir versuchen, ständig neue HF-Relais zu entwickeln und dabei die derzeitige Bandbreite und den aktuellen „Stand der Technik“ zu erweitern. Da immer höhere Frequenzen verwendet werden und Komponenten für die Entwicklung dieser Schaltungen benötigt werden, besteht ein Bedarf an Reed-Relais wie der CRF-Serie und an weiteren Leistungsverbesserungen gegenüber den bestehenden Daten. Unsere Ingenieure sind bereit für diese Herausforderung!